１−１．光電子分光の原理

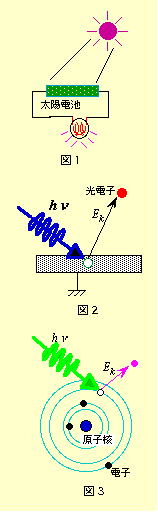　まずは「太陽電池」を思いだしてください。時計や電卓などで太陽電池はよく使われていますが、太陽電池というのは図１のように光をあてる事によって電池の役割を果たすものです。このような機能は「光電効果」（図２）といって、物質に光をあてると物質中の電子が光（光子）からエネルギーをもらって物質から飛び出せるようになる、という性質を利用しています。この光電効果というのは１９世紀後半に現象として知られていましたが、そこでの実験事実を説明する為にアインシュタインがノーベル賞をもらうきっかけとなった「光量子仮説」を提唱したのが1905年の事です（相対性理論でノーベル賞を取っているのではないのです）。「光量子仮説」は、それまで「光は波である」という当時確立されていた概念に真っ向から対立する「光は粒子性をもつ（光子）」という考え方であるだけでなく、今日でも割と当たり前のように考えている「エネルギーの連続性」にも疑問を提起したものでした。そしてそこから「量子力学」の建設につながり、２０世紀の物理学は急激に大きな変化と進歩をとげます。これは単なる学問の発展だけでなく、今日の工業社会、あるいは情報社会への発展の基礎にもなっているものです。

　ちょっと横道にそれましたね。光電効果にもどりましょう。光電効果を、よりミクロに、原子レベルで考えると図３のように考えることができます。原子核のまわりを回っている電子がエネルギーhνの光子を吸収する事で余計にエネルギーをもらい、原子から飛び出す事ができるようになる、という感じです。これをエネルギー保存則で表すと、電子の元々の力学的エネルギー（これは正の電荷を持つ原子核から受けるクーロン引力及び原子核のまわりを回っている時の運動エネルギーが起源です）を-E_B、光子を吸収して飛び出していった時の電子（これを光電子と呼びます）の運動エネルギーをE_kとするとエネルギー保存則より、

となります。ここで力学的エネルギーの基準は電子と原子核の距離が無限大の時のエネルギーを０としています。これを真空準位と呼びます。電子は原子核の近くにいる方が安定でエネルギーが低く、元の力学的エネルギーは負となりますので、ここであらかじめ負の符号をつけました。よってE_Bは正になります。

　次に我々の研究室で行っている固体の光電子分光について解説します。図２のように、接地した試料に単色の光、すなわち一定のエネルギーhνを持つ光をあてます。すると固体中の電子はエネルギーをもらって運動エネルギーE_kの光電子として外に飛び出します。光電子分光とは、この光電子を観測する手法です。もう少し具体的に言うと、色んなエネルギーをもった多数の光電子から、ある運動エネルギーだけをもったものだけを選別して、その光電子の数を数える。そして次に選別する運動エネルギーを少しだけ変えて、その変えたエネルギーの光電子数を数える。さらにまた少しだけ運動エネルギーを変えて．．．という事を繰り返していくと、横軸に光電子の運動エネルギー、縦軸に観測された光電子数というグラフ、光電子のエネルギー分布が得られます。このエネルギー分布を測定する実験が光電子分光です。また、得られたエネルギー分布を光電子スペクトルと呼びます。
　ではこのようにして測定した光電子スペクトルから何が分かるのでしょうか？大地の電位を基準にした電子の元の力学的エネルギーを-E_Bとすると、エネルギー保存則から先の式とは少し違う E_k = hν - E_B - φ が成り立ちます。ここでφとは「仕事関数」と呼ばれる一定のエネルギーで、物質によって値は変わりますが通常数eV（電子ボルト、10^-19ジュール程度）の大きさです。この式をみると、hνとfがあらかじめ分かっていれば、E_kから逆算して電子の元の力学的エネルギーが求められます。ですから、「光電子の運動エネルギー分布」である光電子スペクトルは「電子の元の力学的エネルギー分布」でもあることになり、結局これによって固体中の電子の状態が分かる、という事になります。実際に固体の光電子分光実験は、色々な固体中の電子状態を調べるという目的で行なわれる事が多々あるのです。

このページはAkira Sekiyamaが作成、運営しています。
このページ及び内容の無断転載を禁じます。