ここではちょっと「固体結晶の電子状態」を離れて電子の正体というか性質について説明します。以前「０−２．光は波ってよく言うけど．．．」で「光は波動性と粒子性の両方をもつ。波動、粒子という概念は人間の頭で考えられたイメージでもあり、光がどちらかの状態になる訳ではない」、さらに「電子も波としていいのか？」と書いていますが、ここでは「電子を波として考えてもよい」ということについて触れます。
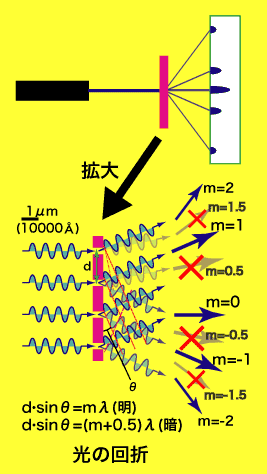
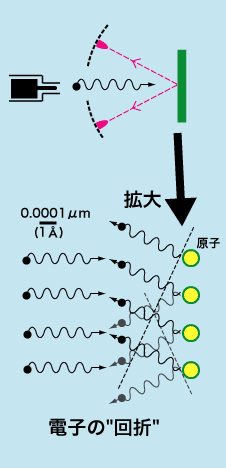では何かが「波」だ、というときにどういう現象がおきれば波と「認定」されるのでしょうか？これは19世紀までの光の波動説と粒子説の論争のよりどころになったところでもあって、光は波だと一旦は決着した（もちろんそれは20世紀に入って再度覆るのですが）のは、「波として考えないと干渉、回折の説明がつかない」からです。光の回折というのは私が高校生の時には物理で必ず学習することでして、図のように小さい穴（スリット）がやはり狭い間隔でいくつもあいている所に光を通すと光の元の進行方向以外の方向にも幾つか明るい点が観測される、という現象です。これは元の光が折れ曲がって、さらに隣の穴から出てきた（波としての）光の山同士、谷同士が揃って強め合う方向に明るい光が生じると説明できます。これは波としての性質の顕著な例です。では電子が波だというからには同じような「回折」が生じなくてはいけませんが、それが実際に観測されたのは20世紀に入ってからです。それも図に示していますが、金属結晶、すなわち周期的に原子が並んだ物質の表面に電子を外から当ててやると、（単純な入射反射の条件以外の）ある特定の角度方向にやたら電子が飛んでくる、という現象です。これは電子線回折とよばれる現象ですが、もしも電子が粒子としての性質をもっているとすると、物質に向けて飛ばした電子は乱反射で跳ね返るとしても四方八方ばらばらに反射して、特定の方向に強め合って飛ぶという事はないはずです。このような現象から、「電気の粒」だと考えられた（現在でもそういうイメージが強いのですが）電子が波としての性質を持つことが確かめられました。このような波としての性質（波動性）というのは電子だけではなく、およそ全ての物質に（人間の体まで含めて！）共通して存在する性質なのですが、ではなぜにその事が人間の歴史のなかで長いこと認識されなかったのか、というとその波長の短さにあります。物質を波として考えた「物質波」の波長は、量子力学によれば（プランク定数）／（物質の運動量）となります。ここで運動量というのは高校の物理で出てくる（物質の質量）×（物質の速度）という運動量そのものです。仮に体重50kgの人間が秒速2m/sで走ったとするとその人の運動量は100kgm/sとなるのですが、その時の波長は、プランク定数が6.6×10-34Jsなのでだいたい6.6×10-36メートルとなり、とてつもなく短いものです。物性物理でよく出てくる長さの単位はオングストロームですが、1Åは1×10-10メートルですから、この走る人の波長の短さは物性物理の世界でも「対象外」な短さで、波としては意識できないのです。ですが電子１個となると大体質量が9×10-31kgで、軽いだけに動く速さもかなり速くなれますからちょっと電圧を1000V位かけて真空中で飛び出させると（ごく大雑把に計算すると）0.4Åの「電子波」になります。そうすると上の電子線回折の例で言えば物質表面の原子間隔は（物質によりますが）数Åと電子波の波長よりも長くなり、その結果回折現象が観測される、ということになります。
この電子の波動性という性質は、物性物理（に限らず現代物理・科学）において重要なものでして、ミクロな世界で見せる（しかもそれが人間の目にもハッキリと観測される）様々な現象を説明し、かつそれを生かして新しい機能を持った物質を開発する、というような局面でも必要不可欠なものです。
